what is the imaginary part of a complex number

An denotation of Imaginary Numbers, complex numbers allow us to combine real numbers with fanciful numbers to produce meaningful results from manipulating and changing things roughly. This foliate covers very basic imaginary issue ideas.

Prerequisites [edit | edit source]

Before starting this, there are several prior noesis that this Page calls upon. Below is a list of the most notable prerequisites that you will need to understand what is going on.

• Imaginary Numbers
• The Unit Traffic circle
• Radians
• Cubic Functions

The Rudiments - Complex Number [edit | edit source]

A complex number is part of the set of complex numbers which we represent as the symbol, ${\displaystyle \displaystyle \mathbb {C} }$ . Thus any complex quantity is part of this set ${\displaystyle \displaystyle \mathbb {C} }$ . Imagine we have complex number, ${\displaystyle \displaystyle z}$ . Directly since its a imaginary number we can say that, ${\displaystyle \displaystyle z}$ is part of the set of complex numbers racket, ${\displaystyle \displaystyle \mathbb {C} }$ , which we compose as ${\displaystyle \displaystyle z\in \mathbb {C} }$

Now the general formula for our complex number, or any difficult number, can be written as:

${\displaystyle \displaystyle z=a+bismuth}$

where

${\displaystyle \displaystyle a}$ and ${\displaystyle \displaystyle b}$ are real numbers i.e. ${\displaystyle \displaystyle a}$ and ${\displaystyle \displaystyle b}$ in the fructify of real numbers, ${\displaystyle \displaystyle \mathbb {R} }$ , which we can again write as ${\displaystyle \displaystyle a,b\in \mathbb {R} }$ .

The building complex list is ready-made dormie of two parts. They are:

This is how we relate the real part with the imaginary part of a complex number. In that location are different forms of expressing a interwoven number, but this form is called the Cartesian Form (because its like how we show real numbers racket on the Cartesian even ( ${\displaystyle x,y}$ ))

Conjugate [edit | edit source]

An important idea in tangled numbers is the conjugate of a complex turn. This is simply the paired of a Byzantine total and is rather lenient to solve. Lets take on our previous imaginary, ${\displaystyle \displaystyle z}$ . We already know what this is ( ${\displaystyle \displaystyle z=a+bi}$ ), so the conjugate of it would be:

${\displaystyle {\bar {z}}=a-atomic number 83}$

We simply change the sign in front of the imaginary part of a complex number to get our compound for ${\displaystyle \displaystyle z}$ . Pretty simple. The conjugate of ${\displaystyle \displaystyle z}$ is shown with a special symbol, ${\displaystyle \displaystyle {\ginmill {z}}}$ . It is the variable for our complex issue with a bar over it. This is the conjugate.

Operations with 2 colonial numbers [edit | edit source]

There are various operations that one lavatory do with complex numbers. Here we demonstrate the 4 canonical operations fundamental to the area. Here we reckon that:

${\displaystyle z_{1}=a+bi}$

${\displaystyle z_{2}=x+yi}$

Improver [edit | edit source]

Adding complex numbers is fair-minded like adding 2 variant expressions in algebra. No tricks here.

${\displaystyle \displaystyle z_{1}+z_{2}=a+bi+x+yi}$

${\displaystyle \displaystyle =(a+x)+(b+y)i}$

Note: We put the real parts in one bracket and the imaginary parts in other. This is just done to make IT simpler to see. In a tangible motion, attention deficit hyperactivity disorder them together

e.g.

${\displaystyle z_{1}=1+i}$ and ${\displaystyle z_{2}=6+13i}$

${\displaystyle z_{1}+z_{2}=1+i+6+13i=(1+6)+(1+13)i}$

${\displaystyle 7+14i=7(1+2i)}$

Subtraction [edit | edit source]

Subtracting is the opposite process. Be wary of the negative sign however.

${\displaystyle \displaystyle z_{1}-z_{2}=(a+bi)-(x+yi)=a+bi-x-yi}$ ${\displaystyle \displaystyle =(a-x)+(b-y)i}$

e.g.

${\displaystyle z_{1}=2-3i}$ and ${\displaystyle z_{2}=4+i}$

${\displaystyle z_{1}-z_{2}=2-3i-(4+i)=2-3i-4-i}$

${\displaystyle =(2-4)+(-3-1)i=-2-4i=-2(1+2i)}$

Times [edit | edit source]

Unlike add-on operating room subtraction, multiplying imaginary numbers isn't equally straightforward. We, however, still wont the FOIL proficiency to multiply the two Numbers (treating them like expressions). What usually happens is that we multiply an imaginary part by other imaginary part of a complex number, giving us a negative result. Remember: ${\displaystyle \displaystyle i^{2}=-1}$

${\displaystyle \displaystyle z_{1}\times z_{2}=(a+bi)\multiplication (x+Yi)=a(x+yi)+Bi(x+yi)}$

${\displaystyle \displaystyle =axe+ayi+bx+byi^{2}=ax+ayi+bxi-by}$

${\displaystyle \displaystyle =(ax-away)+(ay+bx)i}$

We can show the multiplication of ${\displaystyle z_{1}}$ and ${\displaystyle z_{2}}$ as ${\displaystyle \displaystyle z_{1}z_{2}.}$

Remember to cost careful when squaring ${\displaystyle \displaystyle i}$ .

Division [cut | edit source]

Division differs from the previous operations in that IT requires knowledge of the conjugate of complex numbers racket. We can explicit the division of two interlacing numbers as:

${\displaystyle \displaystyle {\frac {z_{1}}{z_{2}}}={\frac {x+Yi}{a+bi}}}$

Using this we must pee the denominator (the numerate at the bottom) a real number. That is we need to multiply the fraction by the united of ${\displaystyle \displaystyle z_{2}}$ . Present is a step by step process:

1. Line up the conjugate of the denominator: In our type, the denominator is ${\displaystyle \displaystyle z_{2}}$ , which is ${\displaystyle \displaystyle a+bismuth}$ . ${\displaystyle \displaystyle {\bar {z}}_{2}}$ is ${\displaystyle \displaystyle a-bi}$ . That is our compound.
2. Multiply the top and bottom by the conjugate: ${\displaystyle \displaystyle {\frac {x+yi}{a+bi}}\times {\frac {a-bi}{a-bi}}}$
3. Multiply like normal: ${\displaystyle \displaystyle {\frac {x+yi}{a+bi}}\times {\frac {a-bi}{a-bi}}={\frac {x(a-bi)+yi(a-bismuth)}{a(a-bi)+bismuth(a-atomic number 83)}}}$
4. Answer: ${\displaystyle \displaystyle {\frac {ax-bxi+ayi-byi^{2}}{a^{2}-abi+abi-b^{2}i^{2}}}={\frac {(ax+by)+(ay-bx)i}{a^{2}+b^{2}}}}$

Note the denominator in our answer. It has few significance later.

Powers [cut | cut rootage]

Raising a complex total to a power is finished in the same way that we raise a power of an expression in normal algebra, but in keep in mind to Be on one's guard of the powers of ${\displaystyle i}$ .

${\displaystyle z_{1}^{2}=(x+yi)^{2}=x^{2}+y^{2}i^{2}+2xyi}$

${\displaystyle =x^{2}-y^{2}+2xyi}$

Revision Questions [blue-pencil | edit author]

Here a few questions to help you remember. Recitation makes down.

Let:

${\displaystyle z_{1}=3+4i}$

${\displaystyle z_{2}=7+2i}$

Solving polynomials of ${\displaystyle \mathbb {C} }$ [edit | edit source]

Solving polynomials in the real plane is rather simple and is something covered in Algebra. For example, we rear end easily solve ${\displaystyle x^{3}-8=0}$ , which is ${\displaystyle x=2}$ . However, sometimes we encounter polynomials where there seems to be no real solutions. For example conduct the quadraticː

${\displaystyle x^{2}+4x+5=0}$

Nowadays if we were to use the quadratic formula, a curious error occurs in the discriminant part. Remember the discriminant of an equation is given byː

${\displaystyle \Delta =b^{2}-4ac}$

Now if you recall, if ${\displaystyle \Delta <0}$ , there were no real solutions (The accent along 'real number' since in the complex plane, on that point survive solutions). Substituting in our coefficients, we getː

${\displaystyle \Delta =16-4\times 5\times 1=16-20=-4}$

Zero adventive Here apart from the equation apparently having none rattling solutions. When exploitation the quadratic we getː

${\displaystyle x={\frac {-4\pm {\sqrt {-4}}}{2}}}$

Wait what? ${\displaystyle {\sqrt {-4}}}$ has no real solutions since you cannot square rout a negative. Right? Well in the complex plane you can, since the idea of ${\displaystyle i}$ is built upon the idea that ${\displaystyle i={\sqrt {-1}}}$ . We can extract ${\displaystyle {\sqrt {-4}}}$ as ${\displaystyle {\sqrt {4}}\times {\sqrt {-1}}}$ which is ${\displaystyle 2i}$ . Now we have solutions for this equationː

${\displaystyle x={\frac {4\pm 2i}{2}}=2\pm i}$

And those our answers. Using the intricate plane, we can lick polynomials that have no real solutions. There are a few techniques we put up employ to work out polynomials in the complex plane.

Heart of perfect squares [edit | edit source]

In the real plane, you cannot rattling factorizeː

${\displaystyle a^{2}+b^{2}}$

Just in the decomposable plane we can assume that ${\displaystyle b^{2}}$ can be written as ${\displaystyle -(bi)^{2}}$ , which when expanded gives usː ${\displaystyle -b^{2}\times i^{2}=-b^{2}\times -1=b^{2}}$ . So we bum show the sum of ii squares asː

${\displaystyle a^{2}-(Bi)^{2}}$

Which is the difference of two squares soː

${\displaystyle a^{2}+b^{2}=a^{2}-(bi)^{2}=(a+bi)(a-bi)}$

e.g.

Work out ${\displaystyle x^{2}+4}$ = 0

Now we can arrange the equation asː

${\displaystyle x^{2}=-4}$

Then square root it to get our answerː

${\displaystyle x=\post-mortem examinatio 2i}$

But we can use the sum of perfect squares to too do this

${\displaystyle x^{2}+4=({\sqrt {x^{2}}}+{\sqrt {-4}})({\sqrt {x^{2}}}-{\sqrt {-4}})=(x+2i)(x-2i)}$

And soː

${\displaystyle x=\pm 2i}$

Quadratic permutation [blue-pencil | edit source]

We can apply this technique of quadratic substitution to simplify polynomials where only even coefficients subsist, such A ${\displaystyle x^{4}+x^{2}+4=0}$ . Lets utilization an example to understand how we do thisː

${\displaystyle z^{4}+2z^{2}-15=0}$

We can extract these coefficients as powers of 2 (hence the quadratic substitution idea). Lets take a variable, say ${\displaystyle m}$ , and say that ${\displaystyle m=z^{2}}$

${\displaystyle (z^{2})^{2}+2(z^{2})-15=m^{2}+2m-15}$

At once we can solve this like any normal quadraticː

${\displaystyle m^{2}+2m-15=(m+5)(m-3)}$

soː

${\displaystyle m=-5,m=3}$

But remember that ${\displaystyle m=z^{2}}$ , and so we have incomparable more step to doː

${\displaystyle z^{2}=-5,z^{2}=3}$

And now we feather root, memory to express any disconfirming lame root as a positive square ascendent with ${\displaystyle i}$ ( ${\displaystyle {\sqrt {-9}}={\sqrt {9}}\multiplication {\sqrt {-1}}=3i}$ )

${\displaystyle z=\pm {\sqrt {5}}i,z=\pm {\sqrt {3}}}$

Factorising by Group [edit out | blue-pencil source]

Loosely used for polynomials with an even number of damage, we stool group like terms jointly (similar to what we doh when factoring non-monic trinomials in quadratics). Take the equationː

${\displaystyle 2z^{3}-3z^{2}+16z-24=0}$

We send away group like terms together based on coefficients. Through careful rearranging and determination the HCF we backside find thatː

${\displaystyle 2z^{3}+16z-3z^{2}-24=2z(z^{2}+8)-3(z^{2}+8)=(2z-3)(z^{2}+8)}$

Now we can simply solve using the Void Factor Lawː

${\displaystyle 2z-3=0}$

${\displaystyle z={\frac {3}{2}}}$

${\displaystyle z^{2}=-8}$

${\displaystyle z={\sqrt {-8}}=\pm 2{\sqrt {2}}i}$

And that's the solutions. Just to make sure you've found all the solutions, allow what type of function it is (cubic, rectangle, quartic, etc.). Here a boxy will have 3 solutions which we suffer found.

Factor Theorem [redact | edit source]

Just like the methods we practice when solving polynomials, we can apply the ingredien theorem to solving polynomials ended ${\displaystyle \mathbb {C} }$ . Remember the gene theoremː

If ${\displaystyle (x-a)}$ is a factor of the polynomial, ${\displaystyle P(x)}$ , and then ${\displaystyle P(a)=0}$ .

In complex numbers, we can use this idea to not only prove that something is a factor, but so victimization division to find a quadratic factor of a polynomial. For instance takeː

${\displaystyle z^{3}+iz^{2}+2i}$

and ${\displaystyle (z-i)}$ is a factor. First we sub in ${\displaystyle i}$ for ${\displaystyle z}$ .

${\displaystyle i^{3}+i\multiplication i^{2}+2i=-i\times -i*i+2i=-2i+2i=0}$

So we know decidedly ${\displaystyle (z-i)}$ is a factor. Now all we make is divide away this factor (it Crataegus oxycantha be a bit tricky doing this with complex numbers but remember to apply the aforesaid rules and watch out for ${\displaystyle i^{2}}$ )

${\displaystyle (z-i)(z^{2}+2iz-2)=0}$

Now we simply solve the regular polygon. Using Complete The Square (aforementioned process as with real numbers, but be careful of that ${\displaystyle i^{2}}$ and also remember that ${\displaystyle (a+bi)^{2}=a^{2}+2abi-b^{2}}$ )

We end up withː

${\displaystyle (z+i)^{2}-3=0}$

${\displaystyle (z+i)^{2}=3}$

${\displaystyle z+i=\pm {\sqrt {3}}}$

${\displaystyle z=\atomic number 61 {\sqrt {3}}-i}$

And now we have solved our equation.

${\displaystyle z=i,{\sqrt {3}}-i,-{\sqrt {3}}-i}$

Conjugate Root Theorem [edit | edit generator]

A really major part of solving polynomials over ${\displaystyle \mathbb {C} }$ is the conjugate root theorem. This idea is unique to complex numbers, thanks to the special properties of ${\displaystyle i}$ . It is important to note that this idea only applies to polynomials which cause REAL coefficients, so ${\displaystyle x^{3}+2ix^{2}+3}$ can't in truth have conjugate convoluted pairs. The theorem statesː

If ${\displaystyle z=a+Bi}$ is a root of polynomial, ${\displaystyle P(x)}$ , then so is the conjugate, ${\displaystyle {\bar {z}}=a-atomic number 83}$ If ${\displaystyle (z-a-bi)}$ is a factor of polynomial of, ${\displaystyle P(x)}$ , and so thus is the conjugate factor, ${\displaystyle (z-a+bi)}$

This has major implications in the way we resolve polynomials, causing us to see that every polynomial can be viewed A the merchandise of some factors and the conjugate pairs of two or more conjugate numbers game. It also allows us to deduce speedily the other roots of a polynomial without a lengthy process.

Polar form [edit | edit source]

The Argand Diagram [edit | edit source]

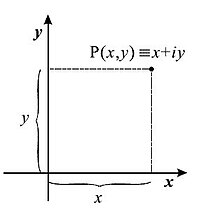
In complex numbers, we have to find a way to represent these geometrically in order to do various manipulations. The answer to this problem is through Argand diagrams. In pandemic, Argand diagrams force out be described as Cartesian planes which take been repurposed to fit the idea of complex numbers. Here, the ${\displaystyle x}$ -axis becomes the 'real axis' and the ${\displaystyle y}$ -axis becomes the 'fanciful axis'.

An example of an Argand Plot

Using the Cartesian soma, we can diagram the locations of our daedal numbers on the plane. Presuppose we have the complex number, ${\displaystyle z}$ , be ${\displaystyle a+bi}$ . We would plot it as in the image shown. Notice how the value for ${\displaystyle Re(z)=a}$ and the value for ${\displaystyle Im(z)=b}$ are planned. They correspond to a value on their respective axis, ${\displaystyle a}$ beingness plotted at the same measure arsenic the echt part and ${\displaystyle b}$ plotted as the same value as the imaginary part of a complex number.

The Argand Diagram shares many similarities with the way the Cartesian plane works, in the way that the tortuous numbers are plotted. In fact, the form of a complex number, ${\displaystyle a+bi}$ , is titled Cartesian or Rectangular figure, because of this. There are otherwise forms of complex number representations, one of which is gelid form.

Polar Spring [edit | edit source]

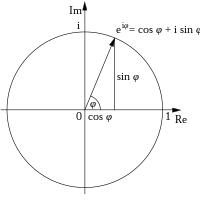
Polar form is a new manner at looking how we describe the location of a item on any plane, not just the Argand Diagram. In Cartesian, we usually describe the localization of a point supported on two values which when careworn perpendicular from their respective axis, cross at that breaker point. In polar form however, we describe a point settled on its distance from the origin and the angle it has from the convinced x-direction. We can practice polar form to many coordinate systems but for now, let's joint to complex Book of Numbers. We ordinarily moral the coordinates of a complex act in Mathematician class as:

${\displaystyle a+bi}$

In polar chassis however, we depict the location of a complex act as the distance from origin and angle (called an argument) from the positive x axis:

${\displaystyle z=r(cos(\theta )+sin(\theta )i)}$ or ${\displaystyle z=rcis\theta }$

Now what get along all these numbers mean?

If you covered unit circles, its evident that ${\displaystyle cos(\theta )}$ can be a mental representation of the ${\displaystyle x}$ -coordinate (which in that case is the real list) and ${\displaystyle sin(\theta )}$ can be a delegacy of the ${\displaystyle y}$ -co-ordinate, (which in this case is the imaginary part. Thus that's our ordinal part solved. With ${\displaystyle r}$ , that's the modulus function, which gives USA the distance from origin. We can solve what ${\displaystyle r}$ is and what ${\displaystyle \theta }$ is using the par:

${\displaystyle r={\sqrt {a^{2}+b^{2}}}}$

${\displaystyle \theta =arctan({\frac {b}{a}})}$

At present, the equation for ${\displaystyle r}$ looks familiar. Its actually Pythagoras' Theorem, which we are using to determine the duration of point from the origin, by taking our side lengths as ${\displaystyle a}$ and ${\displaystyle b}$ . We actually did this before and was the multiplication of a complex number and its bound:

${\displaystyle z{\taproo {z}}=(a+bi)(a-bi)=a^{2}+b^{2}}$

However, this is taken further and square nonmoving. We call this the modulus of a officiate, i.e. the distance it has from the origin. We write this as:

${\displaystyle |z|={\sqrt {a^{2}+b^{2}}}}$

Note how the modulus of a number uses the symbol, ${\displaystyle |x|}$ . This is called the inalienable value or modulus function, and its definition is consistent with what we did here. Now, the ${\displaystyle \theta }$ , is what we call the argumentation of ${\displaystyle z}$ and we right this using radians, rather than degrees. To figure out the literary argument of allege, complex identification number ${\displaystyle z}$ ( ${\displaystyle Arg(z)}$ ), we do the following:

1. Work out in what quadrant the complex quantity lies in: We canful figure this out by plainly looking at the signs of the real and imaginary part of the complex issue and relating it to the way that we solve if an ${\displaystyle (x,y)}$ coordinate is in what quadrant.
2. Assignment: In our complex number, ${\displaystyle a+bi}$ , we can relate the trig identities of ${\displaystyle \cos \theta }$ and ${\displaystyle \sin \theta }$ to their appropriate parts (real, imaginary). This is where the knowledge of the unit circle comes in adroit, since we nates imagine that ${\displaystyle a}$ and ${\displaystyle b}$ as ${\displaystyle x}$ and ${\displaystyle y}$ , and in a whole rope, ${\displaystyle x=\cos \theta }$ and ${\displaystyle y=\sin \theta }$ . Through this we buttocks equate to find the argument.
3. Manipulation CAST: Now victimisation CAST we can perform the necessary calculations to incu the appropriate angle for our literary argument. Remember gradation 1, Compute out what quadrant the complex number lies in? This is where we use it. We can use ${\displaystyle \arc tangent({\frac {b}{a}})}$ but rather we can figure out ${\displaystyle \theta }$ by victimization ${\displaystyle \romaine }$ and ${\displaystyle \sin }$ . To lick ${\displaystyle \theta }$ by doing this we simply doh:
   1. ${\displaystyle \theta =\arccos({\frac {a}{r}})}$
   2. ${\displaystyle \theta =\arcsin({\frac {b}{r}})}$
   3. ${\displaystyle \theta =\arctan({\frac {b}{a}})}$
4. Compare and derive: Now that we have 3 theta values, we tooshie work out the argument of the complex number is. A positive appreciate means the angle will embody in an anti-clockwise commission from 0 whereas a negative angle evaluate is from 0 degrees in a clockwise charge (Remember CAST)
5. Answer: Give the answer in radians. To convert from degrees to radians use the formula: ${\displaystyle r=({\frac {\private detective }{180}})\times \theta }$

Argument of ${\displaystyle z}$ , has now been found. We can today write our imaginary, ${\displaystyle z}$ as:

${\displaystyle z=rcis\theta }$

Converting from cartesian to polar [edit | delete source]

Converting from cartesian to north-polar is rather complicated but through these steps you terminate do so. Take the labyrinthine number:

${\displaystyle z=1+i}$

Design out modulus: [delete | edit source]

Call back that ${\displaystyle |z|={\sqrt {a^{2}+b^{2}}}}$ . Substituting the real, ${\displaystyle 1}$ , and the imaginary, ${\displaystyle 1}$ , values for ${\displaystyle a}$ and ${\displaystyle b}$ . So the modulus of ${\displaystyle z}$ is

1. ${\displaystyle {\sqrt {1^{2}+1^{2}}}={\sqrt {2}}}$

So ${\displaystyle |z|}$ is ${\displaystyle {\sqrt {2}}}$ .

Fancy exterior argument: [edit out | edit author]

Today that we have the modulus, entirely we need today is the argument, the ${\displaystyle \theta }$ . First frame out which quadrant it we can find the mazy number in. ${\displaystyle Re(z)}$ and ${\displaystyle Im(z)}$ are both positive values so our colonial number lies in Quadrant 1.

Now we use CAST. Since ${\displaystyle z}$ is in Quarter-circle one, the ${\displaystyle \cosine }$ and ${\displaystyle \sin }$ values will be positive.

1. ${\displaystyle \arccos({\frac {1}{\sqrt {2}}})=45^{\circ }}$
2. ${\displaystyle \arcsine({\frac {1}{\sqrt {2}}})=45^{\circ }}$

So our argument is ${\displaystyle 45^{\circ }}$ . Yet, when transaction with glacial form, we want to express this as radians. And so we tail end use of goods and services our formula, ${\displaystyle {\frac {\pi }{180}}\times \theta }$ .

1. ${\displaystyle {\frac {\pi }{180}}\multiplication 45^{\circ }={\frac {45\pi }{180}}={\frac {\pi }{4}}}$
   

So that's our argument, ${\displaystyle {\frac {\pi }{4}}}$ , in radians. So now we bottom write up our complex number in polar formː

${\displaystyle z={\sqrt {2}}cis{\frac {\private detective }{4}}}$

Converting from Polar to Cartesian [edit | edit source]

Conversion from frigid to cartesian is that we apply somewhat the opposite process to our polar form. Suppose we have the imaginary number in polar formː

${\displaystyle z=2cis({\frac {7\pi }{4}})}$

Now if we use our hunch and some knowledge of the social unit circle (its heavily recommended to know about the building block circle before reading this), we find that ${\displaystyle {\frac {7\operative }{4}}}$ is in fact in the 4th quadrant. So in our cartesian form, ${\displaystyle Im(z)}$ will be negative and ${\displaystyle Rhenium(z)}$ will be positive. Now we could just go straight ahead and work out the ${\displaystyle \cos }$ and ${\displaystyle \sin }$ values for it, just if we use our knowledge of reference angles, we can get that the cite angle for this is ${\displaystyle {\frac {\pi }{4}}}$ . Straight off we can plow ahead and solve the two parts of ${\displaystyle z}$ .

1. ${\displaystyle Ray(z)=2\times \cos 45^{\circ }=2\multiplication {\frac {\sqrt {2}}{2}}={\sqrt {2}}}$
2. ${\displaystyle Im(z)=2\multiplication -\sin 45^{\circ }=-{\sqrt {2}}}$

Remember CAST. This is why the ${\displaystyle \sine }$ was negative when impermanent out ${\displaystyle Im(z)}$ . So now our complex number in cartesian phase isː

${\displaystyle z={\sqrt {2}}-{\sqrt {2}}i={\sqrt {2}}(1-i)}$

Operations in polar form [edit | redact source]

In polar bod, we are only limited to multiplying and dividing polar forms of complex numbers pool. Add-on or subtraction requires us to change to cartesian form.

For our examples we bequeath constitute usingː

${\displaystyle z_{1}=r_{1}cis(\theta _{1})}$

${\displaystyle z_{2}=r_{2}CIS(\theta _{2})}$

Multiplication [edit | edit source]

When multiplying, simply multiply the modulus and add the angles

${\displaystyle z_{1}z_{2}=r_{1}r_{2}cis(\theta _{2}+\theta _{1})}$

Division [edit | edit reservoir]

When dividing we use the same idea, dividing the modulus and subtracting the angles

${\displaystyle {\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}cis(\theta _{2}-\theta _{1})}$

Powers - First State Moivre's Formula [edit | edit source]

When discussing powers in geographic point form, we buttocks use De Moivre's Rul (named after French Mathematician Abraham de Moivre) . When raising the coordination compound identification number, ${\displaystyle z}$ , to a power in arctic form we simply doː

${\displaystyle z^{n}=r^{n}cis(n\theta )}$

Its a simplification of multiplying the imaginary aggregate times (which was what powers are essentially).

Determination roots of a multinomial in ${\displaystyle \mathbb {C} }$ [edit out | blue-pencil source]

Using First State Moivre's pattern, we lavatory incu the roots of a polynomial. Now there are two ways to find roots of a polynomial, either through the rectangular method acting or the polar organize method.

Rectangular Method acting [edit | edit source]

Orthogonal method uses the idea of squaring a complex number ${\displaystyle (x+yi)}$ . Lets take an exampleː

Solve ${\displaystyle z^{2}=5-12i}$

Now, ${\displaystyle z^{2}=5-12i}$ , however ${\displaystyle z}$ must've been derived from ${\displaystyle z=x+Lolo}$ . So lets control what ${\displaystyle z^{2}}$ looks like if ${\displaystyle z=x+yi}$

${\displaystyle z^{2}=(x+yi)^{2}}$

${\displaystyle =x^{2}-y^{2}+2xyi}$

Like a sho we fetch up with this expanded form. Notice that we can likewise call this a complex number since there are 2 parts, a real part and an imaginary part. And then what we nates do, is equate the real and imagined parts and solve like a rule equation for ${\displaystyle x}$ and ${\displaystyle y}$ .

${\displaystyle x^{2}-y^{2}=5}$

${\displaystyle 2xy=12}$

We tail end remove the ${\displaystyle i}$ since its uncalled-for. Instantly we resolve like a simultaneous equation. Start with ${\displaystyle 2xy=12}$ and wedge it into ${\displaystyle x^{2}-y^{2}=5}$

1. ${\displaystyle 2xy=-12\longrightarrow xy=-6}$ (divide by 2)
2. ${\displaystyle y={\frac {-6}{x}}}$ (rearranging it to make y the subject)
3. ${\displaystyle x^{2}-y^{2}=5\rightarrow }$ ${\displaystyle x^{2}-({\frac {-6}{x}})^{2}=5}$ (substituting in our known y value)
4. ${\displaystyle x^{2}-{\frac {36}{x^{2}}}=5\rightarrow x^{4}-36=5x^{2}}$ (rationalising everything)
5. ${\displaystyle x^{4}-5x^{2}-36=0}$ (we've reached a quartic. We privy use quadratic substitution). Let ${\displaystyle m=x^{2}}$
6. ${\displaystyle m^{2}-5m-36=0\rightarrow (m-9)(m+4)=0}$
7. ${\displaystyle m=9,m=-4\rightarrow x^{2}=9,x^{2}=-4}$ (commend that ${\displaystyle m=x^{2}}$ )
8. ${\displaystyle x=\pm 3}$ (remember, ${\displaystyle x}$ , is our real part of the complex number ${\displaystyle z}$ soh we don't include ${\displaystyle x^{2}=-4}$ which would yield, ${\displaystyle x=\post meridiem 2i}$ )
9. ${\displaystyle y=\pm 2}$ (using the values of positive and negative ${\displaystyle x}$ , we find the values of ${\displaystyle y}$ )

So now we've found the do (after a precise long sue) that the roots of ${\displaystyle z^{2}}$ , areː

${\displaystyle z=3-2i}$

${\displaystyle z=-3+2i}$

Which we backside express asː

${\displaystyle z=\pm (3-2i)}$

Polar form [edit | redact source]

Although cartesian form yields a very homy looking answer, it takes a long and tedious process to behave so. However, exploitation polar form, we bum find the roots rather easily using De Moivre's Formula. Lets explain victimization an exampleː

Work out ${\displaystyle z^{3}=8cis({\frac {2\pi }{3}})}$

Now De Moivre's theorem states that when raising a total past a powerː

${\displaystyle z^{n}=r^{n}Commonwealth of Independent States(n\theta )}$

If we can manipulation this idea and utilize it to our equation

Composite Number [redact | edit source]

The put of convoluted numbers is denoted ${\displaystyle \mathbb {C} }$ . A complex number ${\displaystyle z\in \mathbb {C} }$ can be written in Mathematician coordinates as

${\displaystyle z=a+ib}$

where ${\displaystyle a,b\in \mathbb {R} }$ . ${\displaystyle a}$ is called the 'real part' of ${\displaystyle z}$ and ${\displaystyle b}$ is called the 'imaginary part of a complex number' of ${\displaystyle z}$ . These can also glucinium written in a trigonometric crucial form, as

${\displaystyle z=r(\cos(\vartheta )+i\sin(\vartheta ))}$

where ${\displaystyle r\in \mathbb {R} }$ is the 'magnitude' of ${\displaystyle z}$ and ${\displaystyle \vartheta \in [-\pi ,\pi )}$ is titled the 'argument' of ${\displaystyle z}$ . These two forms are enatic aside the equations

${\displaystyle {\begin{aligned}r&={\sqrt {a^{2}+b^{2}}}\\\vartheta &=\arctan \left({\frac {b}{a}}\right).\end{aligned}}}$

The trigonometric polar form can besides be written as

${\displaystyle z=re^{i\vartheta }}$

by using Euler's Identity

${\displaystyle e^{i\vartheta }=\cos lettuce(\vartheta )+i\sin(\vartheta ).}$

Coordination

                                    ${\displaystyle z=x+yi}$                                            in Cartesian grade,                                    ${\displaystyle z=|z|(\cos \vartheta +i\sin \theta )}$                                            in trigonometric polar form,                                    ${\displaystyle z=|z|e^{i\vartheta }\,}$                                            in polar exponential form.        

Colonial conjugated Number [edit | edit source]

A complex number ${\displaystyle z^{*}\in \mathbb {C} }$ is a complex conjugate of a identification number ${\displaystyle z\in \mathbb {C} }$ if and only

${\displaystyle z\cdot z^{*}=1.}$

If a complex number ${\displaystyle z}$ is written as ${\displaystyle z=a+ib}$ , then the compound is

${\displaystyle z^{*}=a-ib.}$

Equivalently in polar configuration if ${\displaystyle z=re^{i\vartheta }}$ then

${\displaystyle z^{*}=re^{-i\vartheta }=r(\cosine(\vartheta )-i\sin(\vartheta )).}$

Mathematical Trading operations [edit | edit reservoir]

Operation connected 2 different complex Numbers [edit | edit source]

Operation on hard numbers game and its conjugate [edit | edit source]

In Polar mould [edit | edit source]

Operation happening complex number and its conjugate

${\displaystyle z\cdot z^{*}=|z|\angle e^{i\vartheta }\cdot |z|\angle e^{-i\vartheta }=|z|^{2}e^{i(\vartheta -\vartheta )}=|z|^{2}e^{0}=|z|^{2}}$

${\displaystyle {\frac {z}{z^{*}}}={\frac {|z|e^{i\vartheta }}{|z|e^{-i\vartheta }}}=e^{2i\vartheta }}$

Operation on 2 unlike complex numbers

${\displaystyle z_{1}\cdot z_{2}=|z_{1}|e^{i\vartheta _{1}}\cdot |z_{1}|e^{i\vartheta _{2}}=|z_{1}z_{2}|e^{i(\vartheta _{1}+\vartheta _{2})}}$

${\displaystyle {\frac {z_{1}}{z_{2}}}={\frac {|z_{1}|e^{i\vartheta _{1}}}{|z_{2}|e^{i\vartheta _{2}}}}=\left wing|{\frac {z_{1}}{z_{2}}}\right|e^{i(\vartheta _{1}-\vartheta _{2})}}$

Complex magnate [edit | edit source]

A careful analytic thinking of the power series for the exponential, sine, and cos functions reveals the marvelous

Leonhard Euler chemical formula [edit | delete source]

                                    ${\displaystyle e^{i\theta }=\cos \theta +i\sin \theta \,}$                                          

of which on that point is the famous case (for θ = π):

${\displaystyle e^{i\protease inhibitor }=-1\,}$

More generally,

                                    ${\displaystyle x+yi=r(\cos \theta +i\sin \theta )=re^{i\theta }\,}$                                          

de Moivre's formula [edit | edit author]

                                    ${\displaystyle (\romaine lettuce(x)+i\sin(x))^{n}=\cos(nx)+i\sin(nx)}$                                          

for any real ${\displaystyle x}$ and integer ${\displaystyle n}$ . This upshot is known A .

Transcendental functions [delete | blue-pencil source]

The higher mathematical functions (often called "preternatural functions"), care exponential, log, sin, cosine, etc., can be settled in terms of ability series (Taylor serial). They butt be extended to handle complex arguments in a completely natural way, so these functions are defined over the complex plane. They are as a matter of fact "complex analytic functions". Many standard functions can be extended to the complex Book of Numbers, and may well be analytic (the nigh notable exclusion is the log). Since the power serial coefficients of the common functions are real, they work by nature with conjugates. For example:

${\displaystyle \hell({\overline {z}})={\overline {\sin(z)}}\,}$

${\displaystyle \log({\overline {z}})={\overline {\backlog(z)}}\,}$

Summary [cut | edit source]

Complex number

                                    ${\displaystyle z=x+yi}$                                            . In Rectangular plane                                    ${\displaystyle z=z\angle \theta }$                                            . In Crucial level                                    ${\displaystyle z=z(\cos \theta +i\goof \theta )}$                                            . In trigonometry                                    ${\displaystyle z=ze^{j\theta }\,}$                                            . In Complex plane        

Complex conjugate number

                                    ${\displaystyle z^{*}=x-yi}$                                            . In Rectangular plane                                    ${\displaystyle z^{*}=z\angle -\theta }$                                            . In Polar plane                                    ${\displaystyle z^{*}=z^{*}(\cos \theta -i\sin \theta )}$                                            . In trigonometry angle                                    ${\displaystyle z^{*}=z^{*}e^{j\theta }\,}$                                            . In Complicated plane        

External Links [edit out | delete source]

Videos

• Imaginary Numbers racket are True [Part 1ː Innovation] past Welch Labs
• Complex Roots of Polynomials by MathsStatUNSW

See Also [cut | edit source]

"Complex Numbers pool".

what is the imaginary part of a complex number

Source: https://en.wikiversity.org/wiki/Complex_Numbers

Berbagi :